Materi BAB 3 Fungsi Matematika Kelas 10

Baca dan Download ringkasan materi Fungsi SMA Kelas 10 Lengkap. Kamu dapat mendownload rangkuman materi pada akhir pembahasan di laman ini. Silakan Kamu baca dan download materi matematika kelas 10 lainnya di Rangkuman Materi Matematika Kelas 10 Lengkap.
Materi Lain yang berkaitan dengan Matematika kelas 10:
Lihat Juga: Persamaan dan Pertidaksamaan Nilai Mutlak Linear Satu Variabel
Lihat Juga: Sistem Persamaan Linear Tiga Variabel
Lihat Juga: Fungsi
Lihat Juga: Trigonometri
1. 1 Mengenal Apa itu Fungsi
Fungsi matematika merupakan pemetaan setiap anggota sebuah himpunan (dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagai kodomain).
Pada fungsi, terdapat beberapa istilah penting, di antaranya:
- Domain yaitu daerah asal fungsi f dilambangkan dengan Df.
- Kodomain yaitu daerah kawan fungsi f dilambangkan dengan Kf.
- Range yaitu daerah hasil yang merupakan himpunan bagian dari kodomain. Range fungsi fdilambangkan dengan Rf.
1.2 Sifat-Sifat Fungsi
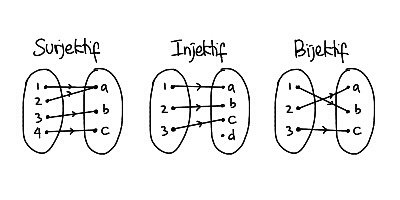
- Fungsi Injektif
Sifat fungsi yang pertama adalah injektif atau juga disebut fungsi satu-satu. Pemetaan (fungsi) f : A → B dikatakan satu-satu atau injektif, jika untuk setiap unsur x1 dan x2 di yang dipetakan sama oleh f, yaitu f(x1) = f(x2) berlaku x1 = x2. - Fungsi Surjektif
Sifat fungsi matematika selanjutnya adalah surjektif.
Fungsi f: A → B disebut fungsi kepada atau fungsi surjektif jika dan hanya jika untuk sembarang b dalam kodomain B terdapat paling tidak satu a dalam domain A sehingga berlaku f(a) = b. Dengan kata lain, suatu kodomain fungsi surjektif sama dengan kisarannya (range). - Fungsi Bijektif
Sifat fungsi matematika yang terakhir ada;ah bijektif. Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu.
1.3 Jenis Fungsi Matematika
- Fungsi Linear
Jenis pertama adalah fugsi linear. Fungsi pada bilangan real yang didefinisikan : f(x) = ax + b, a dan b konstan dengan a ≠ 0 disebut fungsi linear - Fungsi Konstan
Untuk lebih memudahkan anda untuk memahami jenis fungsi yang kedua ini, kami berikan contoh. Misal f:A→B adalah fungsi di dalam A maka fungsi f disebut fugsi konstan jika dan hanya jika jangkauan dari f hanya terdiri dari satu anggota. - Fungsi Identitas
Jenis fungsi berikutnya adalah fungsi identitas. Contoh: f:A→B adalah fungsi dari A ke B maka f disebut fungsi identitas jika dan hanya jika range f = kodomain atau f(A)=B. - Fungsi Kuadrat
Jenis fungsi matematika yang terakhir adalah fungsi kuadrat. Fungsi f: R→R yang ditentukan oleh rumus f(x) = ax2 + bx + c dengan a,b,c ∈ R dan a ≠ 0 disebut fungsi kuadrat.
1.4 Operasi Aljabar pada Fungsi
Secara matematis, jika (f) merupakan suatu fungsi dengan daerah asal (Df), dan (g) merupakan suatu fungsi dengan daerah asal (Dg). Maka operasi aljabar pada fungsi tersebut dapat dinyatakan seperti di bawah:
a. Penjumlahan
f + g didefinisikan sebagai (f+g)(x) = F(x) + g(x):
dengan daerah asal Df+g = Df ∩ Dg
b. Pengurangan
f – g didefinisikan sebagai (f-g)(x) = F(x) – g(x)
dengan daerah asal Df-g = Df ∩ Dg
c. Perkalian
f x g didefinisikan sebagai (fxg)(x) = F(x) x g(x)
dengan daerah asal Dfxg = Df ∩ Dg
d. Pembagian
f : g didefinisikan sebagai (f/g)(x) = F(x) / g(x)
dengan daerah asal Df/g = Df ∩ Dg – {x|g(x)=0}
Contohnya
a. Penjumlahan
f(x) = 7x+8 dan g(x) = 5x+3
Maka (f+g)(x) = 12x+11
b. Pengurangan
f(x) = 7x+8 dan g(x) = 5x+3
Maka (f-g)(x) = 2x+5
c. Perkalian
f(x) = 7x+8 dan g(x) = 5x+3
maka (fxg)(x) = (7x+8)x(5x+3)
d. Pembagian
f(x) = 7x+8 dan g(x) = 5x+3
maka (f/g)(x) = (7x+8)/(5x+3)
1.5 Sifat-Sifat Operasi Fungsi Komposisi
Jika f: R → R , g: R → R: h: R → R, maka berlaku sifat-sifat komposisi sebagai berikut:
- Pada umumnya (fog)(x) ≠ (gof)(x), dikatakan tidak komutatif
- ((fog)oh)(x) = (fo(goh))(x), memenuhi sifat asosiatif
- (foI)(x) = (Iof)(x) = f(x), dengan I adalah fungsi identitas, yakni I(x)=x
Perhatikan contoh berikut!
Jika f(x) = 2x+1,
g(x) = 3x–4, dan
h(x) = x2
Tentukan: a). (fog)(x)
b). (gof)(x)
c). (goh)(x)
d). ((fog)oh)(x)
e). (fo(goh))(x)
f). (Iof)(x)
g) (foI)(x)
Kesimpulan apa yang bisa diperoleh?
Penyelesaian
a). (fog)(x) = f(g(x))
= f(3x-4)
= 2(3x-4) + 1
= 6x – 8 + 1
= 6x – 7
b). (gof)(x) = g(f(x))
= g(2x+1)
= 3(2x+1) – 4
= 6x – 1
c). (goh)(x) = g(h(x))
= g(x2)
= 3x2 – 4
d). ((fog)oh)(x) = (fog)(h(x))
= (fog)(x2)
= 6x2 – 7
e). (fo(goh))(x) = f((goh)(x))
= f(3x2-4)
= 2(3x2-4) + 1
= 6x2 – 7
f). (Iof)(x) = I(f(x))
= f(x)
= 2x + 1
g). (foI)(x) = f(I(x))
= f(x)
= 2x + 1
Dari contoh di atas dapat disimpulkan bahwa:
- (fog)(x) ≠ (gof)(x), tidak komutatif
- ((fog)oh)(x) = (fo(goh))(x)) , memenuhi sifat asosiatif
- (foI)(x) = (Iof)(x) = f(x)
1.6 Fungsi Invers
Fungsi invers memiliki istilah fungsi kebalikan. Fungsi invers adalah suatu fungsi yang berkebalikan dengan fungsi asalnya. Jika fungsi umumnya adalah f, maka fungsi kembalikannya adalah f-1.
Fungsi (f) memiliki fungsi invers (f-1). Apabila (f) adalah satu-satunya fungsi dan fungsi bijektif. Perlu diketahui bahwa fungsi bijektif ditempatkan saat jumlah anggota domainnya sama dengan jumlah anggota kodomain yang dimiliki.
Domain merupakan daerah asam dan kodomain merupakan daerah hasil. Hal ini menjadikan fungsi f memetakan dari A ke B, menjadikan fungsi invers berupa f memetakan dari B ke A.
Umumnya tidak ada dua atau lebih domain berbeda yang dipetakan dalam kodomain yang sama. Perlu diketahui juga bahwa setiap kodomain pasti memiliki pasangan di domain.
1.6.1 Hubungan Fungsi Invers

Hubungan fungsi invers yang dimaksudkan dapat digambarkan sebagai berikut:
(f-1)-1 = f
Contoh yang bisa ditulisakan:
Ketika f fungsi yang memetakan x ke y, sehingga bisa langsung ditulisakan menjadi y = f(x), maka f-1 merupakan fungsi yang memetakan y ke x, ditulis x = f-1(y).
Dapat dimisalkan fungsi f adalah A → B fungsi bijektif. Pada posisi seperti ini, fungsi f adalah fungsi yang menggabungkan pada masih-masing elemen B yang masih tepat satu elemen dengan A.
Ketika fungsi f dinyatakan dengan f-1 maka menjadi sebagai berikut:
f-1 : B → A
Maka akan menjadi,
y = f(x) → x = f-1(y)
1.6.2 Contoh Soal Fungsi Invers
1. Tentukan fungsi invers dari f(x) = 2x² + 5!
Penyelesaian:
f(x) = 2x² + 5y = 2x² + 5
y-5 = 2x²
(y-5)/2 = x²
x = √[(y-5)/2]
f-1(x) = √[(x-5)/2]
2. Tentukan fungsi invers dari g(x) = (2x – 1)/6!
Penyelesaian:
g(x) = (2x – 1)/6
y = (2x – 1)/6
6y = 2x – 1
6y+1 = 2x
x = (6y+1)/2
g-1(x) = (6x+1)/2
3. Tentukan fungsi invers dari h(x) = ³√x+2!
h(x) = ³√x+2
y = ³√x+2
y+2 = ³√x
x = (y+2)³
h-1(x) = (x+2)³
Download Materi PDF
Jika kamu ingin menyimpan rangkuman ini, kamu dapat mendownload ringkasan materi Trigonometri Matematika Kelas 10 ini secara gratis. Silakan mengunduh versi pdfnya melalui link dibawah ini ya:






